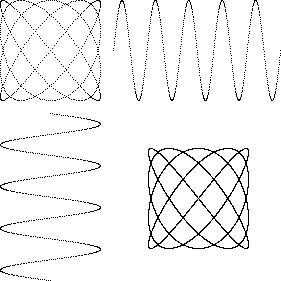
図1:純正律の長3度
図3は平均律のCと平均律のG(391.995 … [Hz])のリサージュである.図2と同じ時間描いてあるから左図のC(横軸)は図2左と同じ点で終っていて,周波数比はほぼ C : G = 2 : 3 であるからCの2周期とGの3周期がほぼ同じ時間になり,その時間の曲線とそれに続く曲線(Cは4周期弱,Gは6周期弱描かれている)がほぼ重なっている.
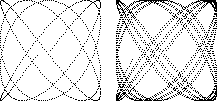
図2:平均律の長3度
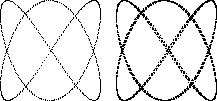
図3:平均律の完全5度
| 〜「数学で出来ている」のは「名曲」ではなく音楽〜 | 6/11, 3/22/13 |
純正律音階と12平均律音階について数理的観点から解説する.いずれの音階でも完全8度の2音(オクターブ)の周波数(1秒間の振動数)比は 1 : 2 であり,純正律音階では完全5度の2音の周波数比を 2 : 3(= 1 : 3/2,例えばソの周波数はドの周波数の 3/2 倍)とする.完全5度の2音で下の方の音(例えばドの下のファ)を完全8度上げると完全4度になるから,純正律音階の完全4度は 3 : 4 となる.一般に周波数比が単純なものほどよく協和する.
| 純正律の長3和音CEG | 自作プログラムで生成 A = 440 [Hz] | 平均律の長3和音CEG |
| (平均律は「うなり」が聴こえる…コンピュータの貧弱なスピーカでは純正律もそのように感じるかも…) | ||
純正律音階
完全8度,完全5度,長3度で構成する.長3度(例えばドとミ)の周波数比は 4 : 5 で,C(ド)の倍音列(一般に周期波形はその基本周波数の自然数倍の周波数を持つ正弦波の合成になっている)にこれらの周波数比を当てはめると,
| 倍音 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | … | 32 | … | 45 | … | 64 |
| 音名 | C0 | C1 | G1 | C2 | E2 | G2 | C3 | D3 | E3 | G3 | B3 | C4 | C5 | F#5 | C6 |
となる(Bは英米).G1 とC2 は完全4度で,その周波数比は 3 : 4,短3度はE2 とG2 から 5 : 6,長6度は 3 : 5 などとなる.長2度はC3 とD3 から 8 : 9(大全音),D3 とE3 から 9 : 10(小全音)の2通りあり,短7度も 5 : 9 と 9 : 16 の2通りある(後者が完全8度に対する大全音に対応).私はポピュラー音楽好きの工学者なので,純正律音階に変化記号の付く音程も含めるのかどうかは知らないが,それらも含めてまとめると,純正律音階の周波数比は次のようになる.
| 音程 | 完全1 | 短2 | 長2大 長2小 | 短3 | 長3 | 完全4 | 増4 減5 | 完全5 | 短6 | 長6 | 短7大 短7小 | 長7 | 完全8 |
| 音名 | C | D♭ | D | E♭ | E | F | F# G♭ | G | A♭ | A | B♭ | B | C |
| 周波数比 | 1 | 16/15 | 9/8 10/9 | 6/5 | 5/4 | 4/3 | 45/32 64/45 | 3/2 | 8/5 | 5/3 | 16/9 9/5 | 15/8 | 2 |
| 1.0666 … | 1.125 1.111 … | 1.2 | 1.25 | 1.333 … | 1.40625 1.4222 … | 1.5 | 1.6 | 1.666 … | 1.777 … 1.8 | 1.875 |
比の一方が5の倍数になっているものは長3度に由来し,そうでないものは完全5度(と完全8度)だけで構成されているが,この2系列があるので,大全音と小全音が生じる.他にも例えば,第 27 倍音はA4,第 81 倍音はE6 になるので,短3度が 27 : 32,長6度が 16 : 27,長3度が 64 : 81 となってしまう(81/64 と 5/4 の比 81 : 80 を syntonic comma と言う).これらは完全5度だけの(長3度を用いない)列からなり,Pythagoras(ピタゴラス)音階と言われる.完全5度の列を続けると,B7 (より B は 243/128),F#9,C#11,G#12,D#14,A#15,E#17 (F17),B#18 (C19) となって,第 312 倍音でCに戻るが,C19/219 = 1.01364 … と若干高くなってしまう(312 : 219 を Pythagorean comma と言う).
長3和音の構成音の周波数比は C : E : G = 4 : 5 : 6 = F : A : C であるが,G : B : D = 4 : 5 : 6 となるのは大全音のときである(小全音のときは 108 : 135 : 160).短3和音では E : G : B = 10 : 12 : 15 = A : C : E であるが,大全音のときは D : F : A = 27 : 32 : 40 となってしまい,10 : 12 : 15 になるのは小全音のときである.Key Cm では,主要3和音の構成音の周波数比がすべて 10 : 12 : 15 になるのは,大全音と短7度の(完全8度に対して)小全音である.また,同じ全音でも,FとGの間やAとBの間の比は 8 : 9,GとAの間の比は 9 : 10 と異なり,大全音の純正律に調律したピアノで Key C の曲を Key G に移調して演奏すると,少なくとも長2度(Gに対してA)の音程が変わってしまう.
小全音と短7度の(完全8度に対して)大全音(Key Cm とは逆の組合せ),増4度を用いて,音名Aの周波数を基準として書き改めると,
| 音程 | 完全1 | 短2 | 長2 | 短3 | 長3 | 完全4 | 増4 | 完全5 | 短6 | 長6 | 短7 | 長7 | 完全8 |
| 音名 | A | B♭ | B | C | C# | D | D# | E | F | F# | G | G# | A |
| 周波数比 | 1 | 16/15 | 9/8 | 6/5 | 32/25 | 4/3 | 36/25 | 3/2 | 8/5 | 27/16 | 9/5 | 48/25 | 2 |
| 1.0666 … | 1.125 | 1.2 | 1.28 | 1.333 … | 1.44 | 1.5 | 1.6 | 1.6875 | 1.8 | 1.92 |
となる.変化記号の付かない音程は Key Cm と一致しているが,音楽の専門家でない私は,変化記号の付く音程,とくにF#とG#が純正律の旋律的短音階や和声的短音階として正しいかどうかは知らない.
12平均律音階
移調を可能にするには,すべての半音の比を同じ値 r (> 0) にすればよく,半音毎の周波数の数列は公比 r の等比数列になり,オクターブは 12 音あるから,r 12 = 2 より r =12√2 = 1.059463094 ….長3度は r 4,完全5度は r 7 などとなり(すべて無理数),12平均律音階の周波数比は次のようになる.
| 音程 | 短2 | 長2 | 短3 | 長3 | 完全4 | 増4 | 完全5 | 短6 | 長6 | 短7 | 長7 |
| 周波数比 | 1.05946 | 1.12246 | 1.18921 | 1.25992 | 1.33484 | 1.41421 | 1.49831 | 1.58740 | 1.68179 | 1.78180 | 1.88775 |
| 平均律に対する 純正律の cent 差 | +11.7 | +3.9 (大) -17.6 (小) | +15.6 | -13.7 | -2.0 | -9.8 (増) +9.8 (減) | +2.0 | +13.7 | -15.6 | -3.9 (大) 17.6 (小) | -11.7 |
最下段は (純正律の cent) - (平均律の cent) = 1200 log2 (純正律の周波数比/平均律の周波数比) を示した("cent" とは完全8度を 1200 とする音程の単位で,平均律では半音が 100 cents,全音が 200 cents になる).工学者は "cent" より "Hz" の世界なので,完全1度(C)の周波数が 264 [Hz] のとき,純正律の長3度の周波数は 330 [Hz],純正律の長6度の周波数は 440 [Hz] となるが,平均律の長3度は約 2.62 [Hz] 高く,平均律の長6度は約 3.99 [Hz] 高くなる.完全4度・完全5度では平均律と純正律の差は約 ±0.5 [Hz] 未満である.
純正律と平均律の違いの視覚化
Aの周波数が 440 [Hz] のとき,純正律のCの周波数は 264 [Hz],純正律のEの周波数は 330 [Hz] となる.図1の左下の波形(通常のグラフを時計回りに 90° 回転していて,縦軸が時間,横軸は振幅)はCで,時間は上端が 0 [s],下端が 1/66 [s] である(ちょうど4周期分で,周波数の逆数が周期だから 4/264 = 1/66).図1の右上の波形はEで,時間は左端が 0 [s],右端が 1/66 [s] である(5/330 = 1/66).図1の左上はCの振幅を x(横軸),同時刻のEの振幅を y(縦軸)として描いてある(リサージュ).図1の右下は 1 [s] まで描いてあるが,周波数比が自然数だから点 (x, y) は同じ軌跡上を動く.
 図1:純正律の長3度 | 図2は平均律のC(261.625 … [Hz])と平均律のE(329.627 … [Hz])のリサージュで,左図は 1/66 [s] まで,右図は 3/66 [s] まで描いてある(Aの周波数は 440 [Hz]).点は中央(時刻 0 [s] の振幅はCもEも 0)より右上に動き,Cの周波数がEの周波数(純正律とほぼ同じ)の 4/5 より低い(逆数の周期は長い)ので左の図では中央の少し左で止まっていて,時間が進むにしたがって右図のように少しずつ異なる軌跡を描く.周波数比が無理数だから決して同じ軌跡に戻ることはなく,点は正方形の領域全体を埋め尽くす(真っ黒の正方形になる). 図3は平均律のCと平均律のG(391.995 … [Hz])のリサージュである.図2と同じ時間描いてあるから左図のC(横軸)は図2左と同じ点で終っていて,周波数比はほぼ C : G = 2 : 3 であるからCの2周期とGの3周期がほぼ同じ時間になり,その時間の曲線とそれに続く曲線(Cは4周期弱,Gは6周期弱描かれている)がほぼ重なっている. | |||
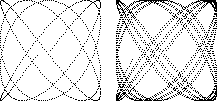 図2:平均律の長3度 | 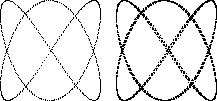 図3:平均律の完全5度 | |||
Guitar の harmonics (ハーモニックス)
弦の長さを変えたとき(太さや張力などは同じ),弦の長さの比の逆数が周波数比になる.例えば完全5度の周波数比は純正律で 3/2 であるから,Guitar の 7th fret とブリッジの間の長さは開放弦の長さの(ほぼ)2/3 になっている.開放弦の基本振動では,両端の点は振動しない節,中央の点は振幅が最大となる腹になる.中央の点(ほぼ 12th fret)も節となるように分割振動をさせると(開放弦を4等分した3点が順に腹,節,腹になる),弦の長さが等価的に 1/2 の振動となり,1オクターブ上の音程の harmonics が鳴る.開放弦の長さの 1/3, 1/4, 1/5, … の点で分割振動をさせると,それぞれの長さに対応した音程の harmonics が鳴る.例えば 7th fret とナットの間の長さは開放弦の長さの(ほぼ)1/3 であるから(節は開放弦を3等分した2点),7th fret で鳴らす harmonics は第3倍音に対応した1オクターブと完全5度上の音程になる.「ほぼ」を3箇所に付けたのは,ブリッジが fret と平行でないため fret とブリッジの長さが弦によって異なるからである.さらに Guitar は平均律の楽器であり,純正律の長3度は平均律よりかなり低いので,第5倍音の harmonics の節は 4th fret よりかなりナット側にある(「ほぼ」を付けたもうひとつの理由).各弦の harmonics の音名は
| fret | 3B | 4N | 5n | 7b | 12 |
| 倍音 | 6 | 5 | 4 | 3 | 2 |
| 1弦E2 | B4 | G#4 | E4 | B3 | E3 |
| 2弦B1 | F#4 | D#4 | B3 | F#3 | B2 |
| 3弦G1 | D4 | B3 | G3 | D3 | G2 |
| 4弦D1 | A3 | F#3 | D3 | A2 | D2 |
| 5弦A0 | E3 | C#3 | A2 | E2 | A1 |
| 6弦E0 | B2 | G#2 | E2 | B1 | E1 |
となる.ここで,fret の後の文字 N は実際の節がナット側,B はブリッジ側にあることを意味し(ブリッジの fret に対する傾斜は考慮していない),それぞれの小文字はその差がわずかであることを意味している.9N の harmonics は 4N と同じ音名になる.第7倍音以上も考えられるが(例えば第8倍音は 8B),うまく鳴らすのは難しい.なお,第7倍音は一般に用いられないそうであるが,増4度に近い 7/5 に対応する点が 6N にある.
harmonics は純正律に基づいているので,5n と 12 の harmonics は平均律と同じ音程であるが,完全5度に対応する 7b と 3B は平均律より少し高く,長3度に対応する 4N はかなり低い.harmonics を利用して平均律の楽器である Guitar をチューニングしても正しく合わせられない.とくに3弦 4N の harmonics に2弦 5n の harmonics を合わせるのが問題となる.実際,電子式チューナ(平均律)で各弦を個別に合わせると,3弦 4N と2弦 5n の harmonics は合っていない.また,7b の harmonics を使う曲(有名どころでは「2?才の別れ」)も,わずかではあるが音程の問題があることになる(もっとも Guitar は構造上の問題でもっと合わない楽器ではあるが).