虚数固有値を持つ線形変換による実平面上の点の像 | 4/20/06 |
平面上の線形変換(1次変換)について,変換を表わす行列の固有値が実数のときの幾何学的意味はよく知られています.固有値が虚数(共役複素数)のときも複素固有ベクトルが複素固有値倍されますが,実平面上の変換としての幾何学的意味が記載されている線形代数の教科書を見たことはありません.固有値が虚数のときは,線形変換と写像したい点によって定まる楕円があって,複素固有値の偏角に相当する楕円上の変換(回転)と複素固有値の絶対値倍(図形の相似変換)との合成写像になります.
定理
平面上の線形変換を表わす2次実正方行列 A の固有値と固有ベクトルを
a ± b i, (a, b は実数,b > 0,i = √-1)
s ± t i (s, t は2次実列ベクトル.複号同順)
とする.s, t を並べた2次実正方行列
P = (s t)
は正則になり,tP -1 P -1 の固有値 α ≦ β は正の実数で,α に対する固有ベクトル u と β に対する固有ベクトル v は直交する.u, v を正規直交基底にとり,
U = (u v)
とする(α = β のときは U = E).写像したい点 p について
r = |P -1 p|
とおき,u を x 軸,v を y 軸とする座標系で,楕円(α = β のときは円)
α x 2 + β y 2 = r 2
を考える.p はこの楕円上の点で,p の像は固有値の偏角に相当する(u, v の向きも考慮した)この楕円上の回転と固有値の絶対値倍との合成で与えられる.すなわち,
c = |a + b i| (= √det A),
θ = arg (a + b i) (0 < θ < π)
とおき,u-v 座標系で,p の座標を
((r/√α) cos φ, (r/√β) sin φ) (= U -1 p)
と表わすと,p の像は
(c (r/√α) cos (φ ± θ), c (r/√β) sin (φ ± θ)) (= U -1 A p).(複号同順) | 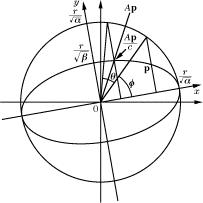
|
ただし,θ の前の複号は det P det U > 0 のとき −,det P det U < 0 のとき + とする.なお,楕円は P の選び方(実数倍)によらず,A と p によってのみ定まる.
3次以上の実正方行列についても,虚数固有値に対する固有ベクトルの実部と虚部の張る平面上で同じことが言える.
以下では,2次正方行列を (a11, a12, a21, a22),2次列ベクトルを (x, y) と表わします.HTML で数式を書くのは困難で,かと言って,画像を多用する(数式を画像にする)のは良くないと思いますし,PDF は嫌いなので,回転と相似変換(原点を中心とする拡大・縮小)の合成になることの証明の概要だけ記します:
B = (a, b, -b, a),R = (cosθ, sinθ, -sinθ, cosθ) とすると,B = c R だから,B は回転変換 R と相似変換(次式も行列の相似変換と言いますが…)の合成で,さらに B = P -1 A P(固有ベクトルの選び方によらないことに注意)だから,q = A p,p' = P -1 p,q' = P -1 q とすると,q' = B p'.また,P R P -1(による p の像が q/c)は,座標変換 (x'', y'') = U -1 (x, y) によって α x'' 2 + β y'' 2 = r 2 と表わされる楕円上の回転を表わす.なお,tP -1 P -1 は対称行列(実 Hermite 行列)だから正規行列で,直交行列(実ユニタリ行列)U によって対角化でき,U は原点のまわりの回転,または,回転と x 軸または y 軸に関する折返しとの合成で,U -1 = tU.
例題
A = (2, 2, -2, 0)
の固有値は 1±√3i だから,その絶対値と偏角は
c = |1+√3i| = 2,
θ = arg (1+√3i) = π/3
となり,固有ベクトルを (2, -1±√3i) / (2√3) ととると,
P -1 = (√3, 0, 1, 2)
である.確かに P -1 A P = (1, √3, -√3, 1) である.
tP -1 P -1 = (4, 2, 2, 4)
だから,その固有値は
α = 2, β = 6
で,座標変換を表わす行列を
U = (1, 1, -1, 1) / √2
ととる.U -1 = tU である.
写像したい点 p が
p = (2, -1)
のとき,
r = |P -1 p| = √12
で,
p'' = U -1 p = (3, 1) / √2
だから,確かに p'' は楕円 2 x 2 + 6 y 2 = 12 上にある .一方,
p'' = √12 ((1/√2) cos φ, (1/√6) sin φ)
だから φ = π/6 となり,det P > 0, det U > 0 だから,
q'' = 2√12 ((1/√2) cos (π/6 - π/3), (1/√6) sin (π/6 - π/3)) = √2 (3, -1).
したがって,
q = U q'' = (2, -4) = A p.
Home へ戻る
