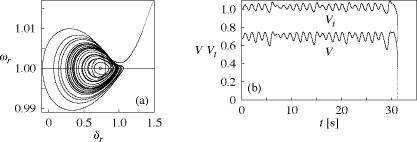
Fig. 7. Voltage collapse at Q1 = 1.26289: (a) projected onto the space with coordinates δr and ωr; (b) V and Vt vs. t.
We vary the reactive power demand Q1 of the load as a parameter to follow [2]. Numerical solutions of the system equations have been computed by means of the fourth-order Runge-Kutta method with time step 0.001 s (= 0.001 ωB [pu]).

Fig. 7. Voltage collapse at Q1 = 1.26289: (a) projected onto the space with coordinates δr and ωr; (b) V and Vt vs. t.
A voltage collapse occurs at Q1 ≅ 1.26289, and a representative orbit and waveforms of voltage collapse are shown in Fig. 7.
At a parameter value smaller than Q1 = 1.26289, the system reaches a voltage collapse or a steady state depending on an initial condition. In order to determine what causes a voltage collapse, we employed the straddle orbit method [10] at Q1 = 1.2628, where the steady state is a period-7 limit cycle, and a straddle orbit was found. We obtained an unstable period-2 orbit at Q1 = 1.26289 by the Newton-Raphson method for Poincare map of the system [9] starting from a point on the straddle orbit. We see that the final part of the orbit shown in Fig. 7(a) moves along the unstable period-2 orbit. It is the unstable period-2 orbit that causes a voltage collapse at Q1 = 1.26289.
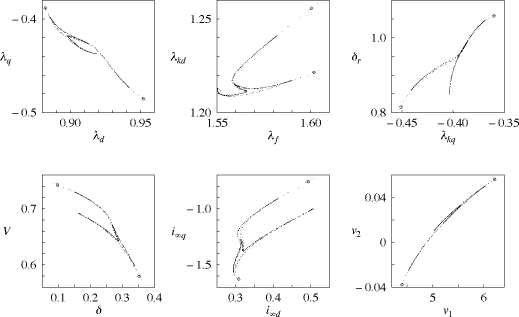
Fig. 9. Poincare map at Q1 = 1.26289 just before voltage collapse; two large circles show the saddle of unstable period-2 orbit, and small dots denote a transient chaotic orbit which tends toward voltage collapse.
Figure 9 shows Poincare maps, where the phase-space coordinate is taken by sampling twelve variables when ωr crosses 1 in the decreasing direction. The pair of large circles in the each figure denotes the saddle point for the map corresponding to the unstable period-2 orbit. Many small dots in the each figure indicate the transient chaotic orbit which touches the unstable period-2 orbit and finally tends toward a voltage collapse. We can confirm by Fig. 9 that the saddle point corresponding to the unstable period-2 orbit is the boundary of a voltage collapse.
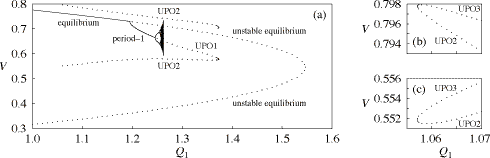
Fig. 10. Bifurcation diagrams showing intersection of solution trajectories with hyperplane of ωr = 1 (dωr/dt < 0), projected onto V, dotted lines represent unstable equilibria or unstable limit cycles. Equilibria, attractors, unstable period-1 orbit (UPO1), and unstable period-2 orbit (UPO2), which causes a voltage collapse, are shown in (a). The unstable period-2 orbit (UPO2) and the other unstable period-2 orbit (UPO3) are shown in (b) and (c).
The bifurcation diagrams including equilibria and unstable limit cycles are shown in Fig. 10(a), where the phase-space coordinate is taken by sampling the load voltage when ωr crosses 1 in the decreasing direction. In Fig. 10(a), swept with Q1 gradually increasing, we see the supercritical Hopf bifurcation clearly. The parameter value of this bifurcation is Q1 ≅ 1.1954. Further swept with Q1 gradually increasing in the figure, we see the branch of limit cycles, with the flip cascade leading to chaos.
The dotted lines labeled UPO2 denote the unstable period-2 orbit which causes a voltage collapse. Note that the unstable period-2 orbit is developed by the Newton-Raphson method for Poincare map, and a straddle orbit converges to it when the value of Q1 is less than 1.26289. The unstable period-1 orbit which originates from the period-1 (stable) limit cycle is also indicated by the dotted line labeled UPO1 in Fig. 10(a). It has another intersection with ωr = 1 and dωr/dt < 0 over Q1 1.371, and the dotted line which represents it in Fig. 10(a) has the other part. In Fig. 10(a), we see the unstable period-2 orbit vanishes with it, and the parameter value of this bifurcation is Q1 ≅ 1.3730. The unstable period-2 orbit also vanishes at Q1 ≅ 1.05713 as shown in Fig. 10(b) and (c). This disappearance is caused by the other unstable period-2 orbit labeled UPO3 in the figures.
The system described in [2] has a pair of equilibria which corresponds to saddle node bifurcation described in [1]. One is stable before the Hopf bifurcation, and the other, the low voltage saddle point, is always unstable. These equilibria also exist in our system as shown in Fig. 10(a), and they vanish at Q1 ≅ 1.5466. In the case of [2], the low voltage saddle point causes a voltage collapse. A transient chaotic motion, which is one of the branches of the unstable manifold of the saddle, escapes from the saddle point along the other branch of the unstable manifold of the saddle, and a voltage collapse occurs. In our system, instead of the low voltage saddle point, the unstable period-2 orbit plays this role. This situation is clearly shown in Fig. 10(a).
The unstable period-2 orbit has one positive characteristic multiplier that is greater than 1, and the absolute values of other characteristic multipliers are less than 1. The unstable period-2 orbit is a saddle point on Poincare cross-sectional 12-dimensional space, and the unstable manifold of the saddle is one-dimensional in the space. The stable manifold of the unstable period-2 orbit, which is 12-dimensional, is the basin boundary between a voltage collapse and a chaotic attractor, a limit cycle, or a stable equilibrium. The saddle point, that is, the unstable period-2 orbit, is the basic set of the basin boundary. A transient chaotic orbit approaches the unstable period-2 orbit along the stable manifold, and escapes from the unstable period-2 orbit along one of the branches of the unstable manifold. After repeating these processes, the orbit moves along the other branch of the unstable manifold, and thus a voltage collapse occurs. See Fig. 9. Because the unstable period-2 orbit has the very large value of characteristic multiplier, 244 in the case of the orbit shown in Fig. 8(a)*, it is hard for a transient orbit to approach the saddle point on Poincare map, and Poincare points are located away from the saddle point.