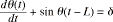 ,
,In this paper we continue earlier studies 1-3 of periodic and chaotic attractors observed in numerical simulations of the delay-differential equation:
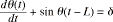 , , | (1) |
where the time delay L and the right hand side δ are constants. This equation is a mathematical model of a phase-locked loop (PLL) with time delay.
Equation (1) can be rewritten in a different form by integrating from an initial time t0 to t:
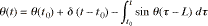 . . | (2) |
In this integral form it is clear that the system acts on initial conditions in the space of integrable functions on some time interval of length L. Since the system (1) is autonomous, the choice of initial time is arbitrary, and we take t0 = 0, so that an initial function is given on [-L, 0]. If the initial function is continuous, a unique solution exists for t > 0 and the solution has a continuous derivative for t > 0; there may be a discontinuity in the derivative of θ at t = 0 (and in higher derivatives at t = L, 2L, ...) unless the initial function satisfies a compatibility condition.
It will be convenient to represent solutions of Eq. (1) or (2) as trajectories projected onto the phase plane with coordinates (θ, dθ/dt). Since the full phase space of the system is an infinite-dimensional function space, we must expect that trajectories projected onto the phase plane may in some instances appear to cross themselves. (In fact for almost all the steady states to be considered here, it seems that the apparent self-crossings could be removed by adding a third coordinate, say d2θ/dt2, to the projection; but see Ref. 3 for phase portraits which suggest structure in more than three dimensions.) In addition to the projected phase plane with -∞ < θ < ∞, it is also useful to consider the cylindrical identification space in which each θ is identified with θ + 2nπ for each integer n, and our phase portraits will be presented in a rectangular region [-π, π) X [δ - 1, δ + 1] unwrapped from the cylindrical identification space. (It is clear from Eq. (1) that dθ/dt will never fall outside [δ - 1, δ + 1].)
The observed steady states may be classified into four broad categories:
(A) Equilibrium points. For |δ| < 1 there are always two, one with θ = Sin-1δ which is stable for L = 0, and another with θ = π - Sin-1δ which is unstable for L = 0. For L > 0, we observe that the second point is always unstable, while the first may be either stable or unstable, depending on the values of L and δ. The stable equilibrium corresponds to tight synchronization of a PLL1.
(B) Limit cycle in the (θ, dθ/dt) plane. When viewed in the cylindrical identification space, this type of orbit closes on itself without making a full net rotation around the cylinder. We call this a limit cycle of the first kind. It would correspond to wobbly synchronization of a PLL.
(C) Limit cycle in the cylindrical identification space which makes one or more full net rotations about the cylinder before closing on itself. This type of orbit is not a closed curve in the original (θ, dθ/dt) plane; it has the property that after one period T, θ(t + T) = θ(t) + 2Nπ for every t, where N is the number of full net rotations. This corresponds to asynchronized operation of a PLL. We call solutions of this type limit cycles of the second kind with rotation N.
(D) Chaotic steady states. Since chaotic steady states contain unstable periodic orbits, it would be possible to further divide the classification of chaotic steady states according to whether they contain only unstable limit cycles of type (B), or only cycles of type (C), or both types of unstable limit cycles.